triphasé |
| 11.1 Généralité
11.2 Tensions triphasées
- 11.2.1 désignation de bornes
- 11.2.2 Raccordement de la ligne au récepteur
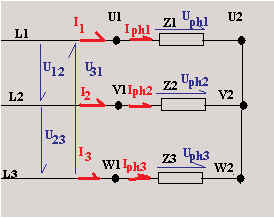
11.3 Désignation des tensions et des courants en
triphasé
couplage étoile
11.4 Récepteur triphasé équilibré couplé en étoile
- 11.4.1 Relation entre courants de ligne et
courants de phase :
- 11.4.2 Relation entre tensions de ligne et
tensions de phase
- 11.4.3 Formules pour le couplage en étoile
- 11.4.4 Absence du conducteur neutre
- 11.4.5 Puissance d’un récepteur équilibré
en triphasé
- 11.4.6 Formules - exemples d'exercices
11.5 Récepteur triphasé non équilibré couplé en étoile
- 11.5.1 Avec conducteur neutre
- 11.5.2 Puissance du récepteur triphasé non
équilibré
11.6 Récepteur non équilibré couplé sans neutre
11.7 Coupure d’un fils
- 11.7.1 Avec conducteur neutre :
- 11.7.2 Sans conducteur neutre
couplage triangle
- 11.8.1 Relation entre tensions de ligne et
tensions de phase
- 11.8.2 Relation entre courants de ligne et
courants de phase
- 11.8.3 Formules pour le couplage triangle
- 11.8.4 Puissance d’un récepteur équilibré
en triphasé
- 11.8.5 Formules - exemples d'exercices
11.9 Rupture d’un fil d’alimentation en triangle
11.10 Mesure de la puissance active
11.11 Amélioration du facteur de puissance
- 11.11.1 Généralités
- 11.11.2 Avantages de l’amélioration du
facteur de puissance
- 11.11.3 Calcul de la capacité des condensateurs
(ce document en pdf)
|
|
.

|
Généralités
sur les circuits triphasé |
11.1.1 Définition tensions triphasées
Un système de tension triphasée est un ensemble de trois
tensions alternatives, de même valeur efficace, décalées l’une par rapport aux
autres de 120°.
un système triphasé peut servir à produire du monophasé (bipolaire)
- 230 V (entre un conducteur polaire et un conducteur neutre )
- 400 V ( entre deux conducteurs polaires)
ou des circuits triphasés multipolaires :
- tripolaire ( uniquement les 3 conducteurs polaires - phases - )
- tétrapolaire ( 3 phases + neutre)
note : le conducteur de protection ne servant qu'à un rôle de protection et ne
conduisant en service normal aucun courant, celui-ci est généralement négligé dans la
théorie de l'électrotechnique même si sa pose est habituellement obligatoire.
11.1.2 Courants triphasés
Dans une installation électrique triphasée, il arrive que les courants eux
n’aient ni la même valeur efficace, ni le même décalage, ni même une forme
sinusoïdale (comme par exemple un courant à travers une lampe économique). Les formules
développées dans ce fascicule ne sont toutefois valables que pour des courants de forme
sinusoïdale.
11.1.3 Avantage du système triphasé
Par rapport au système monophasé, le triphasé permet :
- le transport de puissance avec moins de pertes en ligne.
- une économie de fil conducteur (par exemple : Pour une même masse de cuivre, on peut
transporter plus d’énergie en triphasé)
- d’alimentation de moteurs bon marché (moteur à cage d’écureuil) et facile
d’entretien
- de créer un champ magnétique tournant
- d’avoir plusieurs tensions à disposition (par exemple : 230 et 400 V)
- d’obtenir un faible taux d’ondulation lors de l’emploi de redresseurs.
Pour produire des tensions alternatives triphasées, il faut un alternateur dont on a
disposé les 3 (groupes d’) enroulements statoriques en les décalant de 120° les
uns par rapport aux autres, le rotor étant une source de flux magnétique.
|
|
11.2
Tension triphasée |
| Le réseau électrique alimente une majorité d’usagés avec
un circuit triphasé. Habituellement, la tension entre chaque conducteur polaire
est de 400 V et entre un conducteur polaire et le conducteur neutre une tension de 230
V, mais il existe aussi des réseaux 3*230 V - notamment en Belgique .
Les conducteurs de protection, de terre ou d’équipotentiel sont au même
potentiel que le conducteur neutre dans les système TN et TT ( voir norme) . Leur rôle est
d’assurer la protection. En service normal, ils ne conduisent aucun courant et
n’ont aucune influence dans le circuit du point de vue de la théorie
électrotechnique, nous n’en parlons donc pas dans ces pages.
ci-contre : une représentation vectoriel (chaque vecteur a une amplitude égale à la
valeur de crête de la tension), une représentation temporelle et une indication par les
petits ronds des valeurs instantanées des tensions. |
|
11.2.1 Désignation des bornes
| Les extrémités des enroulements de l’alternateur ou des
impédances d’un récepteur sont repérées par les lettres suivantes : U1 - U2 ; V1 - V2; W1 - W2
On admet que le potentiel le plus élevé est indiqué par
l’indice 1. Le courant s’écoulant donc de U1 à U2, de V1 à V2 et de W1 à W2
dans les impédances est donc considéré comme positif.
11.2.2 Raccordement de la ligne au
récepteur
Le raccordement des conducteurs de ligne aux récepteurs ou aux
alternateurs se fait en connectant les conducteurs :
L1 à la borne U1
L2 à la borne V1
L3 à la borne W1
Le raccordement des bornes de sortie dépend du type de couplage :
étoile ou triangle.
Anciennement, les conducteurs étaient appelés R, S, T et les
bornes U - X ; V - Y; W- Z |
désignations actuelles
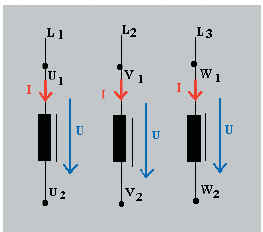
anciennes désignations
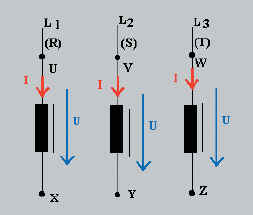 |
Le générateur est un alternateur triphasé.
Les 3 impédances forment soit un récepteur triphasé unique, soit des
récepteurs monophasés placés dans une installation.
Lorsqu’on relie les trois conducteurs de retour des trois circuits
monophasés, ce nouveau conducteur est appelé conducteur neutre. |
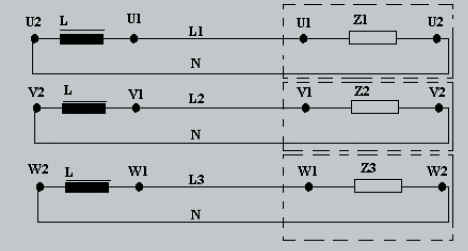 |
|
Les bornes U2, V2, et W 2 sont reliées aux générateurs et aux
récepteurs. Le nombre de conducteurs est ainsi diminué.
|
|
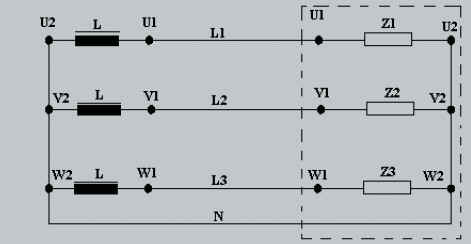 |
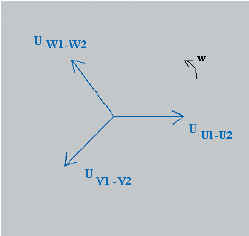 |
Les tensions d’un système triphasé sont définies par
les équations suivantes :
uU1-U2(t)
= U · 20,5 · sin (w· t + 0) [V]
uV1-V2(t)
= U · 20,5 · sin
(w· t – 2p/3) [V]
uW1-W2(t)
= U · 20,5 · sin
(w · t – 4p/3) [V]
Rappels :
- la pulsation ohms est en radian par seconde donc l’angle est en radian
[rad].
- une puissance 0,5 = la racine carré de ...
|
|
|
11.3
Désignation des tensions et des courants en triphasé |
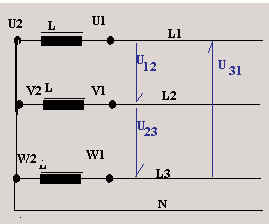
La tension d’alimentation que l’on mesure entre les conducteurs L1 et L2,
entre L2 et L3 et entre L3 et L1 se note U et s’appelle tension composée,
tension de ligne ou tension polaire.
L’usage est que lorsqu’on parle de U en triphasé, on fait référence à la
tension composée.
Cette tension vaut généralement dans le réseau européen 400 V.
UL1-L2 = U12
= 400 [V]
UL2-L3 = U23 = 400
[V]
UL3-L1 = U31 = 400
[V]
Cette notation est souvent utilisée. Elle signifie qu’il y a à disposition trois
tensions (déphasées de 120 °) de 400 V chacune. |
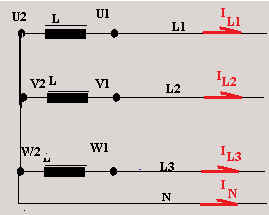
Le courant qui circule dans les conducteurs d’alimentation L1, L2 ou L3
s’appelle courant de ligne ou courant polaire.
Il se note I.
I1 = IL1 [A]
I2 = IL2 [A]
I3 = IL3 [A]
Le courant qui circule dans le conducteur neutre est appelé courant de neutre et noté
: IN |
En triphasé, il existe principalement 2 couplages :
étoile
|
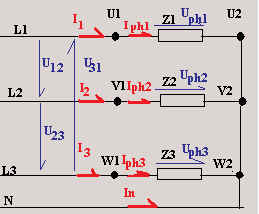
Dans les 2 cas, la tension aux bornes de chacune des impédances est une
tension simple ou tension de phase notée :
Uph [V]
Le courant qui traverse chacune des impédances se nomme courant simple ou courant de
phase noté :
Iph [A]
|
triangle
.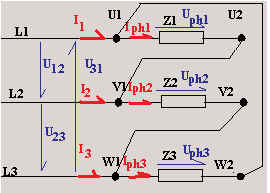 |
|
|
11.4
Récepteur triphasé équilibré couplé en étoile. |
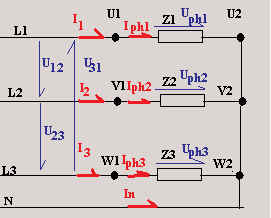
11.4.1 Relation entre courants de ligne et
courants de phase :
Il n’y a aucun nœud entre la ligne et les impédances du récepteur raccordé
en étoile.
Les courants de ligne traversent directement les impédances. Ils ont donc la même
valeur et le même déphasage que les courants de phase. |
 |
11.4.2 Relation entre tensions de ligne et
tensions de phase :
Les tensions de phases Uph sont celles mesurées aux bornes des impédances soit
la tension mesurée entre le conducteur neutre et chacun des conducteurs polaires. |
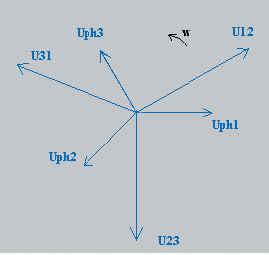
La tension composée est donc la différence de potentiel entre deux tensions de phase.
Les tensions de phase ayant des directions et sens différents, on parle de vecteur
tension et il faut faire une soustraction vectorielle.
U12 - Uph1
+ Uph2 = 0 [V]
U23
- Uph2 + Uph3 = 0 [V]
d'où
U31
+ Uph1 - Uph3 = 0 [V]
|
U12 = Uph1 - Uph2
U23
= Uph2 - Uph3
U31
= Uph3 - Uph1 |
|
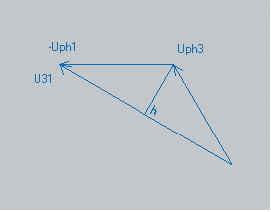
| Les 3 vecteurs forment un triangle
isocèle. La hauteur h partage la base U et deux parties égales . l’angle entre Uph et U est de 30 degrés ( Uph3
et U31 sur le dessin)
La longueur de est :U/2 = Uph · cos 30° |
comme U est 2 fois plus grand
que U/2: U = 2 · U/2 = 2 · Uph
· cos 30° = Uph · 2 · cos 30°.
2 · cos 30° donne un nombre irrationnel qui vaut 30,5.
2 · 0,866 = 1,732 = 30,5
Donc la tension composée vaut :
U = Uph ·
30,5 |
|
11.4.3 Formules pour le couplage en étoile
I intensité du courant de
ligne [A]
Iph intensité du courant de phase [A]
U tension réseau [V]
Uph tension de phase [V]
|
Iph = I
[A] |
Uph = U / 30,5 [V] |
|
Dénominations usuelles
Lorsqu’on désigne un réseau par 3 * 400 V - 50 Hz, cela signifie un réseau à
trois conducteurs polaires sans conducteur neutre. On parle aussi de triphasé tripolaire.
Lorsqu’on désigne un réseau par 3 * 400 /230 V - 50 Hz, cela signifie un réseau
à quatre conducteurs soit 3 conducteurs polaires et un conducteur neutre. On parle aussi
de triphasé tétra polaire
La plus grande des tensions étant la tension du réseau.
Cela indépendamment du conducteur de protection. |
Exemple
La tension réseau est normalisée à 400 V.
Quelles sont les valeurs des tensions de phase?
Solution :
Uph= U / 30,5 = 400
/ 1,732 = 231 [V]
soit 230 [V] normalisé. |
|
Remarque
Comme il s’agit de valeur normalisée, on admet que la tension de phase vaut dans
ce cas 230 V.
En pratique les tensions que l’on mesure sont rarement aux valeurs normalisées car
elles varient en fonction de la charge du réseau.
11.4.4 Absence du conducteur neutre
Dans un couplage équilibré les courants de ligne ont la même intensité et le même
angle de déphasage avec leur tension de phase. La somme des 3 courants à chaque instant
est nul.
Le conducteur neutre ne conduit, dans ce cas, aucun courant et peut être omis (sauf
s’il a un rôle de protection : conducteur PEN). |
 |
11.4.5 Puissance d’un récepteur équilibré en
triphasé :
Dans un circuit équilibré (par exemple un moteur, un chauffe-eau),
les trois impédances sont identiques, ainsi que leurs tensions aux bornes (Uph).
Les courants de phases sont également identiques.
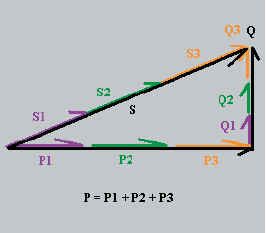
Donc les valeurs des puissances seront égales entre elles.
P = Pph1 + Pph2 + Pph3
= 3 · Pph
Q = Qph1 + Qph2 + Qph3
= 3 · Qph
S =( P 2 + Q 2 ) 0,5
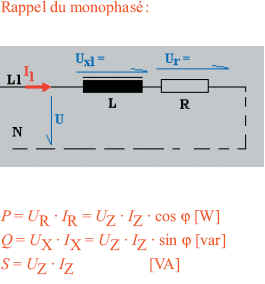
Le calcul des puissances par impédance se fait selon la théorie des
circuits monophasés : |
 |
| La plupart du temps, il est plus facile de mesurer le courant de ligne et la
tension de réseau. Le calcul des puissances devient :
| P |
Q |
S |
= 3 · Pph
= 3 · Uph·Iph
· cos f
= 3 · U/30,5 · I·cos
f
= 3 ·U·I.cos f /30,5
= U · I · 30,5 ·cos f |
= 3
· Qph
= 3 · Uph · Iph
· sin f
= 3 · U/3 0,5 ·I·sin
f
= U · I · 3 0,5· sin f |
= 3
· Sph
= 3 · Uph · Iph
= 3 · U / 3 0,5 · I
= U · I · 3 0,5 |
|
 |
|
U tension réseau [V]
I intensité du courant de ligne [A]
f angle de déphasage [°]
P puissance active triphasée [W]
Q puissance réactive triphasée [var]
S puissance apparente triphasée [VA]
|
| P = U · I · 30,5 ·
cos f [W] |
| Q = U · I · 30,5 ·
sin f [var] |
| S = U · I · 30,5
[VA] |
|
Remarque
Pour raccorder un récepteur triphasé en étoile, il faut vérifier que sa tension de
phase soit de 230 V.
Lorsqu’il y a l’indication de deux tensions comme sur l’exemple à droite,
la tension la plus basse est la tension de phase.
P est la puissance à la sortie du moteur (Putile)
et pour les appareils thermique ou les appareil (perceuse) la puissance absorbée
Applications du couplage étoile :
- enroulements de moteurs ;
- corps de chauffe de radiateur ;
- corps de chauffe de chauffe-eau ;
- corps de chauffe de fours industriels.
|

P = puissance utile ( ou puissance mécanique )
si réseau 3* 400 V entre phases : raccordement étoile
si réseau 3* 230 V entre phases : raccordement triangle
|
raccordement de ce moteur en étoile sur un réseau 3* 400 [V]
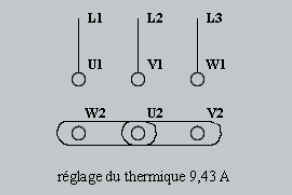 |
Exemple 1
Un moteur triphasé absorbe au réseau une puissance de 2,8 kW sous 3*400 V - 50 Hz,
cos F = 0,85. Ses enroulements sont couplés en étoile.
Calculez :
a) la tension aux bornes de chaque enroulement ;
b) l’intensité du courant de ligne ;
c) l’intensité du courant dans chaque enroulement ;
d) la puissance réactive.
|
 |
 |
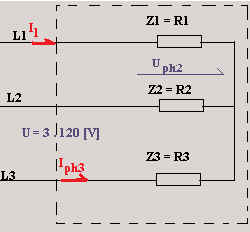
Exemple 2
Trois résistances (R1 = R2 =
R3 = 25 W ) sont couplées en
étoile et raccordées sous 3*120 V.
Calculez la tension de phase, l’intensité du courant de ligne et la puissance
active.
|
|

|
Exemple 3
La puissance d’un chauffe-eau raccordé en étoile au réseau est de 9 kW. Quelle
est la résistance d’un corps de chauffe ?
|
 |
 |
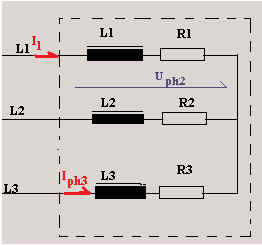
Exemple 4
Un récepteur raccordé en étoile sur le réseau est composé de 3 bobines dont
l’impédance vaut (50 ohms; f=
36,9 [°].)
calculez Pph, P, Q, S, Ur, UXl, I
! |
 |
solution 1
résistance de chaque impédance
R = Z · cos f = 50 · cos 36,9° = 40 [ohms]
tension de phase :
Uph = U/ 3 0,5 =400 / 3 0,5
= 230 [V]
courant de phase et de ligne :
I = Iph=Uph / Z = 230 / 50 = 4,60 [A]
déphasé de 36,9 [°] par rapport à Uph
tension aux bornes de chaque résistance :
UR = Uph · cos f = 230 .
0,8 = 184 [V]
tension aux bornes de chaque réactance :
UXl = Uph · sin f = 230 ·
0,6 = 138 [V]
puissance active par impédance :
Pph = Uph · Iph · cos f = 230 · 4,6 · 0,8 = 846 [W]
Puissance active du récepteur :
P = 3 · Pph = 3 · 846,4 = 2540 [W]
Puissance réactive du récepteur :
Q = 3 · QL = 3 · UXl · IXl
= 3 · 138 · 4,6 = 1900 [var]
Puissance apparente du récepteur :
S = 3 · Sph = 3 · Uph · Iph
= 3 · 230 · 4,6 = 3170 [var] |
solution 2
résistance de chaque impédance
R = Z · cos f = 50 · cos 36,9° = 40 [ohms]
tension de phase :
Uph = U/ 3 0,5 =400 / 3 0,5
= 230 [V]
courant de phase et de ligne :
I = Iph=Uph / Z = 230 / 50 = 4,60 [A]
déphasé de 36,9 [°] par rapport à Uph
tension aux bornes de chaque résistance :
UR = Uph · cos f = 230 .
0,8 = 184 [V]
tension aux bornes de chaque réactance :
UXl = ( Uph2 -UR2
)0,5 = (230 2 184 2)0,5 = 138 [V]
puissance active par impédance :
PR = UR · IR = 184 · 4,6 = 846
[W]
Puissance active du récepteur :
P = U · I · 30,5 · cos f =
400 · 4,6 · 1,73 · 0,8 = 2550 [W]
Puissance réactive du récepteur :
Q = U · I · 30,5 · sin f = 400 ·
4,6 · 1,73 · 0,6 = 1910 [var]
Puissance apparente du récepteur :
S = U · I · 30,5 = 400 · 4,6 · 1,73 = 3180 [var] |
|
|
11.5 Récepteur triphasé non équilibré couplé en
étoile |
11.5.1 Avec conducteur neutre
- Lorsque les courants de phases n’ont ni la même intensité ni le même angle de
déphasage ; le circuit n’est pas équilibré.
- Lorsque les courants de phase ont la même intensité, mais des angles de déphasage
différents, le circuit n’est pas équilibré.
- Lorsque les courants de phase ont le même angle de déphasage, mais des intensités
différentes ; le circuit n’est pas équilibré.
Dans ces trois cas, le conducteur neutre fixe le potentiel aux bornes U2, V2 et W2. Les
3 tensions de phase ont donc la même valeur.
Uph1 = Uph2
= Uph3 |
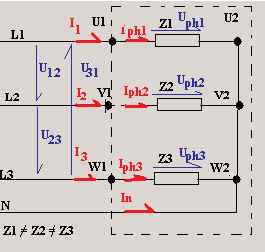 |
Le point neutre représente un nœud et l’on peut y
appliquer la loi de Kirchhoff. Attention, pour pouvoir additionner tous les courants, il
faut les représenter sous leur forme vectorielle. On parle de somme vectorielle (ou
géométrique).
IN + I ph1 + Iph2 + Iph3
= 0 [A]
d'où
IN = - ( Iph1 + Iph2 + Iph3)
|
 |
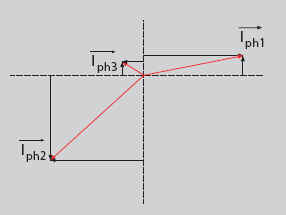 |
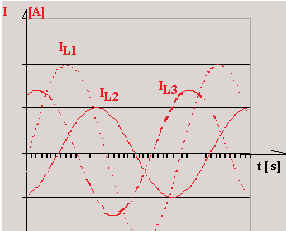
Pour déterminer le courant dans le neutre à l’aide des
vecteurs, on met bout à bout les vecteurs courant (en respectant leur sens, leur
direction et leur amplitude). Le vecteur courant dans le
conducteur neutre est celui qui relie la somme des trois premiers vecteurs à
l’origine.
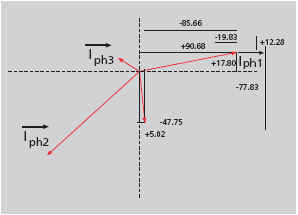
Le calcul du courant dans le neutre peut se faire en décomposant
chaque vecteur courant en coordonnées X et Y selon un système d’axe.
En changeant le signe des sommes des projections X et Y on trouve
les projections du vecteur courant dans le neutre.
Il est très utile d’utiliser les fonctions de transformation
rectangle–polaire et polaire–rectangle des machines à calculer. |
 |
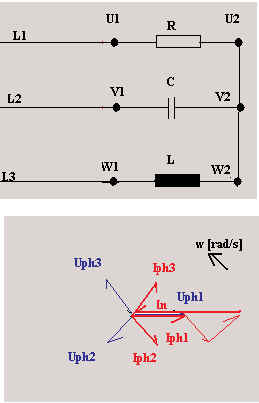
Exemple:
Aux bornes U1-U2 est raccordée une résistance de 23ohms,
entre V1 et V2 un condensateur de 138,4 uF et entre W1 et W2 une inductance de 73,21 mH.
Ce récepteur est couplé en étoile sur le réseau.
calculez
a) le courant dans chaque impédance du récepteur
b) le courant dans le neutre
impédance entre L1 et neutre
Z1 = R1 = 23 [ohms]
impédance entre L2 et le neutre
Z2 = Xc2 = (ohmsC)-1
= (314,2 · 138,4 · 10-6)-1 = 23 [ohms]
impédance entre L3 et le neutre
Z3 = Xl3 = ohmsL =
314,2 · 0,07321 = 23 [ohms]
courant de phase 1
Iph1=Uph1 / Z1 = 230 / 23 = 10 [A] (f = 0 [°])
courant de phase 2
Iph2 = Uph2 / Z2 = 230 / 23 = 10 [A] (f = - 90 [°])
courant de phase 3
Iph3= Uph3 / Z3 = 230 / 23 = 10 [A] (f = 90 [°]) |
| |
I
[A] |
f
[°] |
a
[°] |
Ix
[A] |
Iy
[A] |
Iph1
Iph2
Iph3 |
10
10
10 |
0
-90
90 |
0
-30
30 |
10
8,66
8,66 |
0
-5
5 |
| IN |
27,32 |
|
|
27,32 |
0 |
|
 |
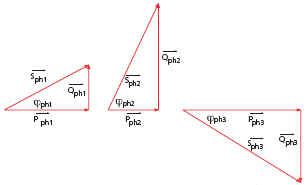
11.5.2 Puissance du récepteur triphasé
non équilibré
Dans ce cas, chacune des puissances doit être calculée individuellement
La puissance active totale est la somme arithmétique des puissances active de chaque
phase.
La puissance réactive totale est la somme algébrique des puissances réactive de
chaque phase.
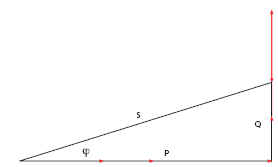
La puissance apparente totale est la somme vectorielle des puissances apparente de
chaque phase. |
|
Formules
P puissance active du récepteur [W]
Pph puissance active d’une impédance [W]
Q puissance réactive du récepteur [var]
Qph puissance réactive d’une impédance [var]
S puissance apparente du récepteur [VA]
Sph puissance app. d’une impédance [VA]
Rappel : le signe de la puissance réactive est positif si l’impédance à un
comportement inductif et un signe négatif pour un comportement capacitif. Toutefois, on
peut inverser la convention, cela ne change pas les résultats. |
| P = Pph1
+ Pph2 + Pph3 [W] |
| Q =
± Qph1 ± Qph2 ± Qph3 [var] |
| S =
(P 2 +Q 2)0,5
[VA] |
|
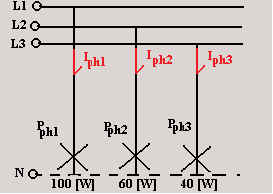
Exemple 1
Trois lampes à incandescence de 100 W, 60 W et 40 W sont raccordées sous 230V, selon
le schéma ci-dessous.
Calculez :
a) l’intensité des courants dans les lampes ;
b) l’intensité du courant dans le conducteur N ;
c) la puissance active totale.
|
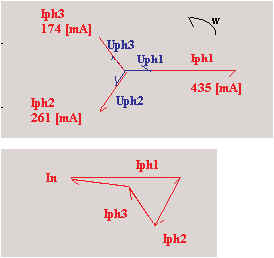
solution :
a) intensité des courants
Iph1= Pph1 / (Uph1 · cosf1) =100 / (230 · 1) = 435[mA]
Iph2 = Pph2 / (Uph2 · cosf2) =60 / (230 · 1)= 261[mA]
Iph3= Pph3 / (Uph3 · cosf3) =40 / (230 · 1)= 174[mA]
b) IN = 0,23 [A]
c) puissance active totale
P = Pph1 + Pph2 + Pph2
= 100+60+40 = 200 [W] |
 |
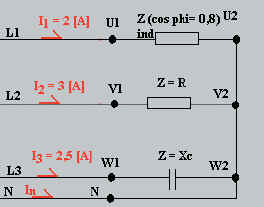
Exemple 2
Calculer pour le couplage ci-dessous:
|
a) L’intensité du courant dans le conducteur
neutre
b) la puissance active totale
c) la puissance réactive globale
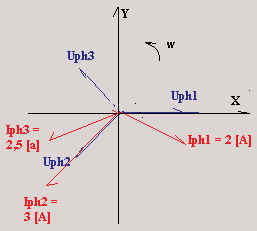
|
a)
l’intensité du courant dans le neutre :
cos f = 0,8 (inductif) => f1
= 36,9 [°]
par calcul :
|
I
[A] |
f
[°] |
a
[°] |
Ix
[A] |
Iy
[A] |
Iph1
Iph2
Iph3 |
2
3
2,5 |
37
0
- 90 |
-37
-120
-150 |
1,6
-1,5
-2,17 |
-1,2
-2,6
-1,25 |
IN |
5,46 |
|
67,7 |
2,07 |
5,05 |
par dessin : voir graphique ci-dessous :
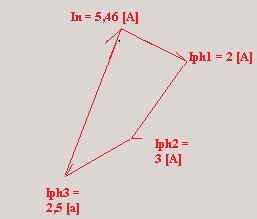
|
b) Pph1 = Uph1 · Iph1
· cos f1 = 230 · 2 · 0,8 = 368 [W]
Pph2 = Uph2 · Iph2
· cos f2 = 230 · 3 · 1 = 690 [W]
Pph3 = Uph3 · Iph3
· cos fph3 = 230 · 2,5 · 0 = 0 [W]
P = Pph1 + Pph2 + Pph2
= 368 + 690 + 0 = 1060 [W]
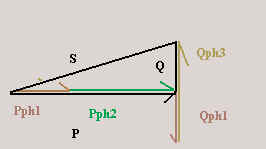
c)
Qph1 = Uph1 · Iph1
· sin f1 = 230 · 2 · 0,6 = 276 [var]
Qph2 = Uph2 · Iph2
· sin f2 = 230 · 3 · 0 = 0 [var]
Qph3 = Uph3 · Iph3
· sin f3 = 230 · 2,5 · (-1)= -575 [var]
Q = Qph1 + Qph2 + Qph3
= 276 + 0 - 575 = -299 [var]
(comportement capacitif) |
Représentation d'une distribution étoile de l’installation électrique.
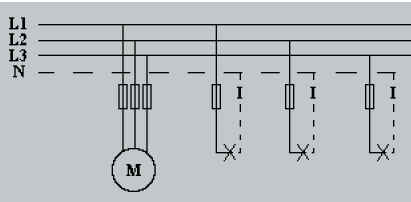
La plupart des récepteurs monophasés sont raccordés au réseau de distribution entre
un conducteur polaire et le conducteur neutre. Ils sont construits pour une tension
nominale de 230 V.
Lors du raccordement des tableaux de distribution, il faut le plus également possible
répartir ces charges afin d’équilibrer au mieux les intensités des courants de
ligne et de diminuer celle du conducteur neutre.
Vus du distributeur d’énergie, ces récepteurs ne représentent qu’un
couplage étoile d’un ensemble d’impédance.
L’interruption du conducteur neutre sans l’interruption des conducteurs
polaires peut entraîner de graves conséquences.
Danger pour les personnes
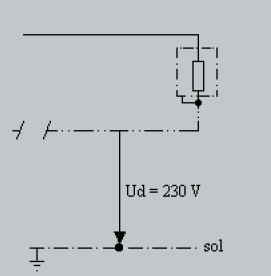
Lorsqu’une installation est réalisée en schéma TN-C (ancien schéma 3), la
rupture du conducteur neutre a pour conséquence la mise sous tension des parties
métalliques du récepteur |
|
Danger pour les récepteurs
Comme pour un couplage série, la coupure du conducteur neutre à pour effet de
répartir les tensions proportionnellement aux valeurs des impédances (un récepteur de
grande puissance subit une diminution de sa tension alors qu’un récepteur de faible
puissance – impédance élevée – la voit augmenter). |
|
|
11.6
Récepteur non équilibré couplé en étoile sans neutre |
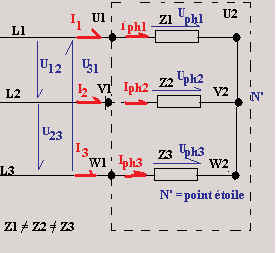
Répartition des tensions de phase
Les trois impédances Z1, Z2 et Z3 ne sont pas
identiques. Les courants de phase Iph1, Iph2 et Iph3
sont différents, leur somme vectorielle vaut toujours zéro et le déphasage entre eux
n’est plus de 120 °.
Les tensions aux bornes des 3 impédances Z1, Z2 et Z3
ne sont plus identiques entre elles, ni égale à la tension de phase d’un système
équilibré et leur déphasage entre elles n’est pas de 120 °.
Le potentiel du point étoile présente une différence par rapport à celui du
conducteur neutre. La valeur de cette différence est d’autant plus importante que
les valeurs des impédances sont différentes.
Le système vectoriel permet de déterminer les valeurs des nouvelles tensions de phase
(selon l’exemple 1).
La méthode décrite n’est utilisable que si les trois impédances provoquent le
même angle de déphasage (f) courant-tension. |
 |
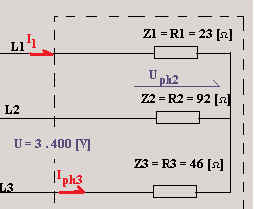
Exemple 1
situation :
Lors d’une intervention sur un tableau de distribution, l’électricien omet
le raccordement du conducteur neutre d’un récepteur triphasé non équilibré.
a) déterminer les tensions aux bornes de chaque résistance
b) calculer l’intensité des courants qui les traverse |
|
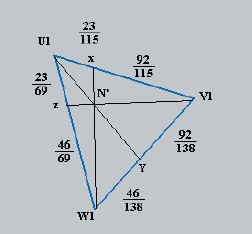
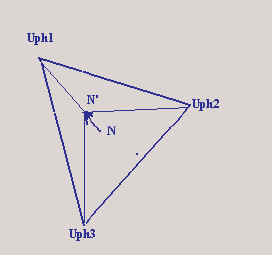
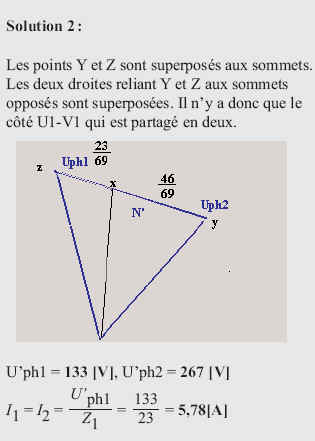
Résolution :
1) tracer le triangle des vecteurs tension de ligne
2) partager U1-V1 proportionnellement aux valeurs des résistances raccordées entre U1
et V1 et noter ce point X ;
partager V1-W1 proportionnellement aux valeurs des résistances raccordées entre V1 et
W1 et noter ce point Y;
partager W1-U1proportionnellement aux valeurs des résistances raccordées entre W1 et
U1 et noter ce point Z ;
3) relier les points X, Y et Z aux sommets opposés.
|
L’intersection de ces trois droites détermine la position du
point étoile N’ (qui n’est plus au même potentiel que le conducteur neutre).
De ce point neutre N’ les trois vecteurs tensions aboutissant aux sommets du
système triphasé représentent les tensions aux bornes des résistances.
U'ph1 = 150 [V]
U’ph2 = 300 [V]
U’ph3 = 260 [V]
Intensité des courants dans les résistances :
I’ph1 =U'ph1 / Z1 = 150 / 23 =
6,52 [A]
I’ph2 = U'ph2 / Z2 = 300 / 92
= 3,26 [A]
I’ph3 = U'ph3 / Z3 = 260 / 46
= = 5,65 [A]
|
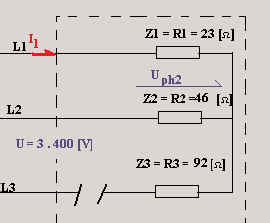
Exemple 2
Dans le montage ci-contre, calculer l’intensité dans les conducteurs L1 et L2
ainsi que la tension aux bornes de R1 et de R2. |
|

|
 |
|
|
11.7
Coupure d'un fils d'alimentation ( récepteur étoile équilibré) |
11.7.1 Avec conducteur
neutre :
a) calculer la puissance active totale avant la coupure du conducteur L3
b) calculer la puissance active totale après la coupure du conducteur L3
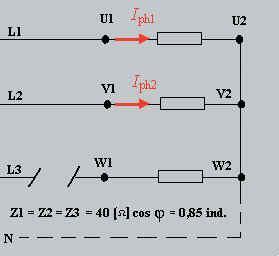
a) puissance active totale avant la coupure
Iph =Uph / Z = 230 / 40 = 5,75 [A]
P = 3 · Uph · Iph · cos f
= 3 · 230 · 5,75 · 0,85 = 3,372 [kW]
b) puissance active totale après la coupure
Iph1 = Iph2 = Uph / Z = 230 /
40 = 5,75 [A]
Pph1 = Pph2 = Uph1 · Iph1
· cos f1 = 230 · 5,75 · 0,85 = 1,124 [kW]
P = Pph1 + Pph2 = 1,124 + 1,124 = 2,248
[kW]
soit les 2/3 de Pnominal |
11.7.2 Sans conducteur neutre
:
a) calculer la puissance active totale avant la coupure du conducteur L3
b) calculer la puissance active totale après la coupure du conducteur L3
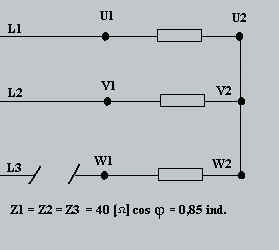
a) puissance active totale avant la coupure
Iph =Uph / Z = 230 / 40 = 5,75 [A]
P = 3 · Uph · Iph · cos f
= 3 · 230 · 5,75 · 0,85 = 3,372 [kW]
b) puissance active totale après la coupure
c’est un circuit série monophasé 400V:
I = U / (Z1 + Z2) = 230 / ( 40 + 40 )= 5
[A]
P = U · I · cos f= 400 · 5 · 0,85 =
1700 [W]
soit la moitié de Pnominal |
|
|
ici
11.8 Récepteur triphasé équilibré couplé en triangle |
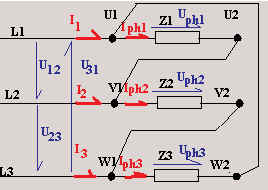
11.8.1 Relation entre tensions de ligne et
tensions de phase
Chacune des impédances du récepteur est raccordée entre deux conducteurs polaires.
Les tensions de phase ont donc la même valeur que les tensions de ligne. |
|
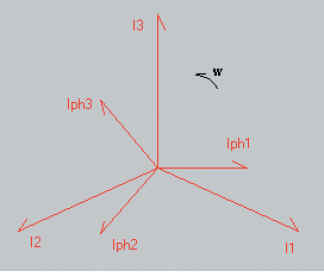
11.8.2 Relation entre courants de ligne et
courants de phase
Les courants de phases Iph sont ceux qui traversent les impédances.
A chaque borne d’entrée, le courant de ligne se partage en deux courants de phase
déphasée de 120 degrés. |
Les courants ayant des directions et des sens différents, on parle de vecteur courant.
Le courant de ligne est la différence entre les deux vecteurs courant de phase
I12 - Iph1
+ Iph2 = 0 [A]
I23 - Iph2
+ Iph3 = 0 [A]
I31 + Iph1
- Iph3 = 0 [A]
|
I12 = Iph2 - Iph1
I23 = Iph3
- Iph32
I31 = Iph1
- Iph3 |
 |
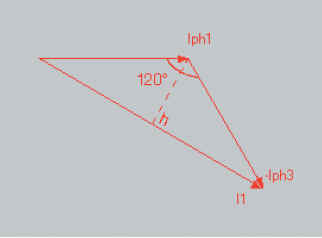
Les 3 vecteurs forment un triangle isocèle. La hauteur h
partage la base I et deux parties égales .
L’angle entre Iph et I/2 est de 30 degrés.
La longueur de est :
I/2 = Iph · cos 30 |
comme I est 2 fois plus grand que I / 2 :
I = 2 · I/2 = 2 · Iph · cos 30 = Iph · 2 · cos 30 = Iph
· 30,5
note :2 · cos 30 [°] donne un nombre irrationnel qui vaut
30,5.
Donc la tension composée vaut :
I = Iph . 30,5 |
 |
11.8.3 Formules pour le couplage triangle
I intensité du
courant de ligne [A]
Iph intensité du courant de phase [A]
U tension réseau [V]
Uph tension de phase [V] |
Iph = I
/ 30,5 [A] |
Uph = U [V] |
|
11.8.4 Puissance d’un récepteur équilibré en
triphasé :
Dans un circuit équilibré (par exemple un moteur, un chauffe-eau),
les trois impédances sont identiques, ainsi que leurs tensions aux bornes (Uph).
Les courants de phases sont également identiques.
Donc les valeurs des puissances seront égales entre elles.
P = Pph1 + Pph2
+ Pph3 = 3 · Pph
Q = Qph1 + Qph2
+ Qph3 = 3 · Qph
S =( P 2 + Q
2 ) 0,5
Le calcul des puissances par impédance se fait selon la théorie des
circuits monophasés :. |
 |
| La plupart du temps, il est plus facile de mesurer le courant de ligne et la
tension de réseau. Le calcul des puissances devient :
| P |
Q |
S |
= 3 · Pph
= 3 · Uph·Iph
· cos f
= 3 · U/30,5 · I·cos
f
= 3 ·U·I.cos f /30,5
= U · I · 30,5 ·cos f |
= 3
· Qph
= 3 · Uph · Iph
· sin f
= 3 · U/3 0,5 ·I·sin
f
= U · I · 3 0,5· sin f |
= 3
· Sph
= 3 · Uph · Iph
= 3 · U / 3 0,5 · I
= U · I · 3 0,5 |
|
 |
|
U tension réseau [V]
I intensité du courant de ligne [A]
f angle de déphasage [°]
P puissance active triphasée [W]
Q puissance réactive triphasée [var]
S puissance apparente triphasée [VA]
|
| P = U · I · 30,5 ·
cos f [W] |
| Q = U · I · 30,5 ·
sin f [var] |
| S = U · I · 30,5
[VA] |
|
Remarque
Pour raccorder un récepteur triphasé en triangle sur notre réseau,, il faut
vérifier que sa tension de phase soit de 400 V.
Lorsqu’il y a l’indication de deux tensions comme sur l’exemple à droite,
la tension la plus basse est la tension de phase.
P est la puissance à la sortie du moteur (Putile)
et pour les appareils thermique ou les appareil (perceuse) la puissance absorbée
Applications du couplage étoile
- enroulements de moteurs
- corps de chauffe de radiateur
- corps de chauffe de chauffe-eau ;
- corps de chauffe de fours industriels.
|
 P =
puissance utile ( ou puissance mécanique )
si réseau 3* 690 V entre phases : raccordement étoile
si réseau 3* 400 V entre phases : raccordement triangle |
raccordement de ce moteur en étoile sur un
réseau 3* 400 [V]
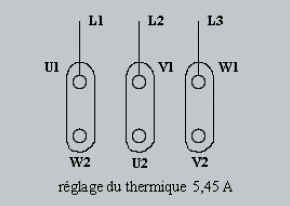 |
Exemple 1
Un moteur triphasé absorbe au réseau une puissance de 2,8 kW sous 3*400 V - 50 Hz,
cos ??= 0,85. Ses enroulements sont couplés en triangle.
Calculez :
a) la tension aux bornes de chaque enroulement ;
b) l’intensité du courant de ligne ;
c) l’intensité du courant dans chaque enroulement ;
d) la puissance réactive.
plaquette moteur
U: 400 / 690 V A / Y
I : 5,45 / 9,43 A P = 5 kW
cos f = 0,8 |
 |
 |
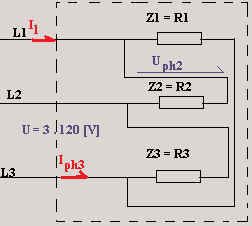
Exemple 2
Trois résistances (R1 = R2 = R3 = 25 ohms) sont couplées en triangle et
raccordées sous 3 · 120 V.
Calculez la tension de phase, l’intensité du courant de ligne et la puissance
active. |
|
impédance : Z = (R et f = 0°) tension
de phase : Uph = U = 120 [V]
Intensité de ligne :
Iph =Uph / Z =120 / 25 = 4,8 [A]
I = Iph · 3 0,5 = 4,8 · 1,73 = 8,30 [A]
Puissance active :
soit :
P = U · I · 3 0,5 · cos f = 120
· 8,3 · 1,73 · 1 = 1720 [W]
soit : P = 3 · Uph · Iph · cos f = 3 · 120 · 4,8 · 1 = 1730 [W] |
Remarque
A impédances identiques, le couplage triangle est trois fois plus puissance que le
couplage étoile.
|
|
11.9
Rupture d’un fil d’alimentation : |
a) calculer la puissance active totale avant la coupure du conducteur L3
b) calculer la puissance active totale après la coupure du conducteur L3
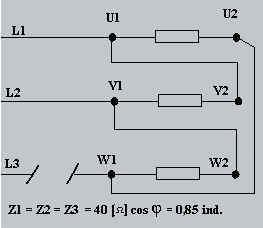 |
a) P = 3 · · cos f = 3
· · 0,85 = 10,20 [kW]
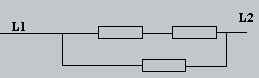
b) Il s’agit d’un couplage monophasé :
Zéqui = Z1 + (Z2 -1 + Z3-1)-1
= 26,67[ohms]
P= U 2 / Zéqui · cos f
=
400 2 · 0,85 / 26,67 = 5100 [W]
soit la moitié de Pnominal |
Il s’agit d’un couplage monophasé :
|
|
|
11.10
Mesure de la puissance active en triphasé |
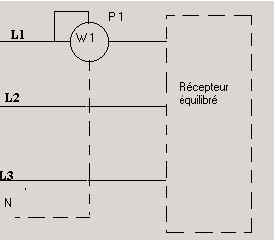
11.10.1 Méthode pour récepteurs
équilibrés
La puissance P, indiquée par le wattmètre est celle d’une phase, pour connaître
la puissance totale active, il faut multiplier cette valeur par trois.
P = 3 · P1 [W]
Si le point neutre n’est pas accessible, il faut le créer à l’aide de trois
résistances équivalentes couplées en étoile, l’une d’entre elle étant celle
du circuit tension du wattmètre.
|
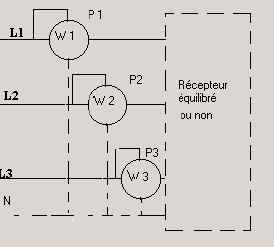
11.10.2 Méthode générale
Chaque wattmètre indique la puissance d’une phase.
La puissance triphasée est la somme arithmétique des puissances lues sur chaque
wattmètre.
P = P1 + P2
+ P3 [W]
Si le point neutre n’est pas accessible, il faut relier en étoile les 3 sorties
des circuits tension des wattmètres, ceux-ci devant avoir la même résistance.
|
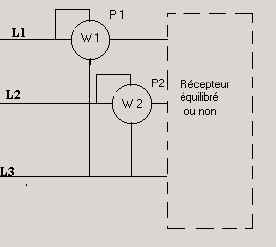
11.10.3 Méthode des 2 wattmètres
Cette méthode permet de mesure la puissance triphasée d’un circuit quelconque
avec ou sans neutre.
P = P1 + P2
[W]
Remarques : Selon le facteur de puissance du circuit mesuré, il se peut qu’un des
wattmètres dévie en sens contraire. Dans ce cas, il faut inverser les connexions du
circuit tension et soustraire la valeur lue de celle de l’autre appareil de mesure. |
|
|
|
11.11
Amélioration du facteur de puissance |
|
Le facteur de puissance est le rapport entre la puissance active et la puissance
apparente d’un circuit.
Le facteur de puissance est assimilable au cosinus de l’angle f
(déphasage courant-tension) si les courants et les tensions sont de forme
sinusoïdale.
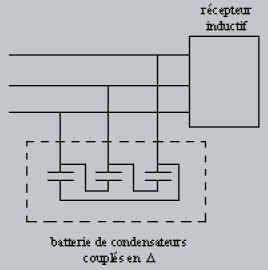
En triphasé, l’amélioration du facteur de puissance s’effectue au moyen
d’une batterie de condensateurs centralisée (batterie de compensation). La puissance
réactive que doit fournir la batterie de compensation est calculée de la même façon
qu’en monophasé. La batterie est composée de trois condensateurs fournissant chacun
un tiers de la puissance réactive capacitive.
Dans le cas particulier de réseau, on peut faire fonctionner un moteur synchrone en
surexcitant son rotor pour produire de la puissance réactive.
L’amélioration du facteur de puissance tend idéalement à lui donner une valeur
proche de 1. En pratique, on se contente d’une valeur proche de 0,9 (inductif).
Les batteries de compensations sont munies de régulateurs qui permettent
d’adapter les besoins d’énergie réactive capacitive en alimentant de façon
successivement les différents échelons de la batterie. Plus le nombre d’échelons
est grand, plus le réglage est fin. |
 |
11.11.2 Avantages de l’amélioration du
facteur de puissance
Pour les sources de tension, à puissance apparente égale, la puissance active
soutirée peut être plus grande avec un facteur de puissance proche de 1.
Pour un circuit inductif, le courant dans la ligne sera plus petit (donc les pertes en
ligne aussi) si on y améliore le facteur de puissance.
Il arrive que les distributeurs facturent l’énergie réactive (usine).

|
11.11.3 Calcul de la capacité des
condensateurs
Pour le calcul de la capacité des condensateurs, il faut d’abord déterminer la
puissance réactive à fournir au total, puis par condensateur.
Exemple:
Un moteur triphasé absorbe un courant de 85 A et crée un déphasage de 50 degrés.
Calculer la valeur de la capacité des condensateurs à brancher en triangle pour avoir un
facteur de puissance de 0,9 au réseau
|
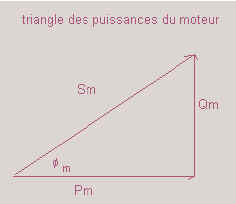
Grandeurs utilisées :
Pm puissance active du moteur [W]
Sm puissance apparente du moteur [VA]
Qm puissance réactive du moteur [var]
fm facteur de puissance du moteur
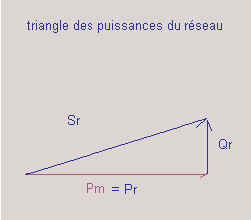
PR puissance active du réseau [W] (= Pm)
SR puissance apparente du réseau [VA]
QR puissance réactive du réseau [var]
fR facteur de puissance du réseau
Sb puissance apparente de la batterie [VA] (= Qb)
Sc puissance apparente d’un condensateur [VA] (= Qc)
Xc réactance de capacité d’un condensateur
C capacité de chaque condensateur
|
Calculs
Pm = U · I · cos fm · 30,5
=
400 · 85 · 0,5 · 1,732 = 29,44 [kW]
Qm = Pm · tg fm
= 29,44 · 1,152 = 35,09 [kvar]
PR = Pm = 29,44 [kW]
QR = PR · tg fR
= 29,44 · 0,4843 = 14,26 [kvar]
Qb = Qm - Qr = 35,09 - 14,26 = 20,83 [kvar]
Qc = Qb / 3 = 20,83 / 3= 6,943 [kvar]
Xc = Uc2 / Qc = Uph2 / Qc
= 4002 / 6943 = 23,04 [ohms]
C= 1 / (2. p. f . Xc ) =1 / (2. p. 50 . 23,04 ) = 138,15 [mF]
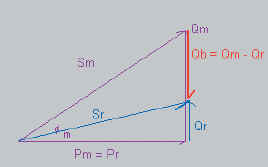
note : Iréseau = 47,22 [A] |
|
|
|